Contextual RNN-GANs for Abstract Reasoning Diagram Generation
Arnab Ghosh*, Viveka Kulharia*, Amitabha Mukerjee, Vinay Namboodiri, Mohit Bansal
*Equal contribution
Motivation
Understanding, predicting, and generating object motions and transformations is a core problem in artificial intelligence.
Modeling sequences of evolving images may provide better representations and models of motion and may ultimately be used for forecasting, simulation, or video generation.
Diagrammatic Abstract Reasoning is an avenue in which diagrams evolve in complex patterns and one needs to infer the underlying pattern sequence and generate the next image in the sequence.
An Example with an Explanation
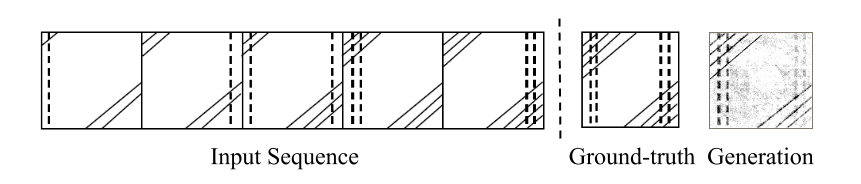
An explanation of the ground truth is that the dashed line first goes to the left, then to the right, and then on both sides, and also changes from single to double, hence the ground truth should have double dashed lines on both the sides. On the corners, the number of slanted lines increase by one after every two images, hence the ground truth should have four slant lines on both the corners.
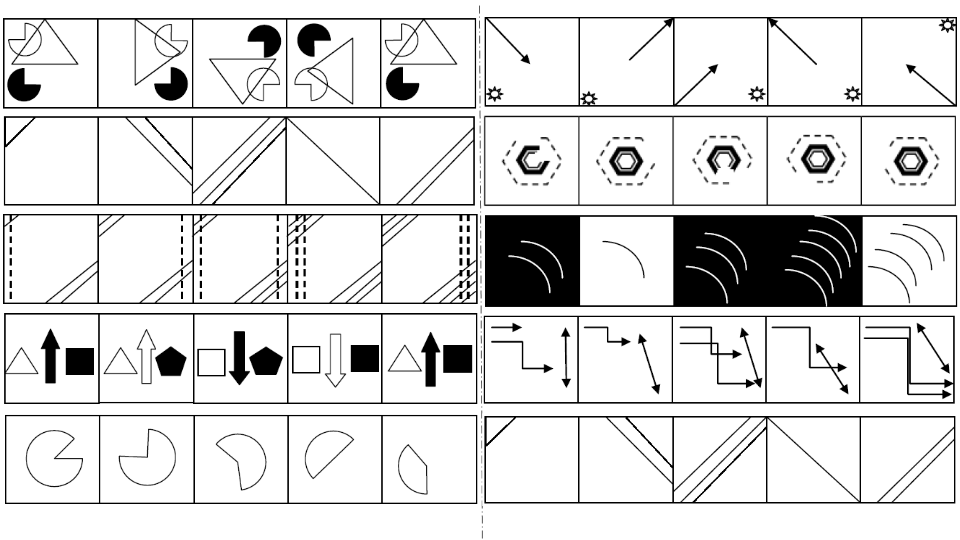
Some More Example Problems From DAT-DAR Dataset
The Model
Contextual RNN-GAN
GANs have been shown to be useful in several image generation and manipulation tasks and hence it was a natural choice to prevent the model make fuzzy generations.
In Context-RNN-GAN, 'context' refers to the adversary receiving previous images (modeled as an RNN) and the generator is also an RNN. The name distinguishes it from our simpler RNN GAN model where the adversary is not contextual (as it only uses a single image) and only the generator is an RNN.
The discriminator is modeled as a GRU-RNN which gets all the preceding images to decide whether the generation by the Generator is the correct image for the timestep.
The generator is modeled as a GRU-RNN which tries to generate an image using the preceding images. It is guided by the contextual discriminator to produce real looking images.
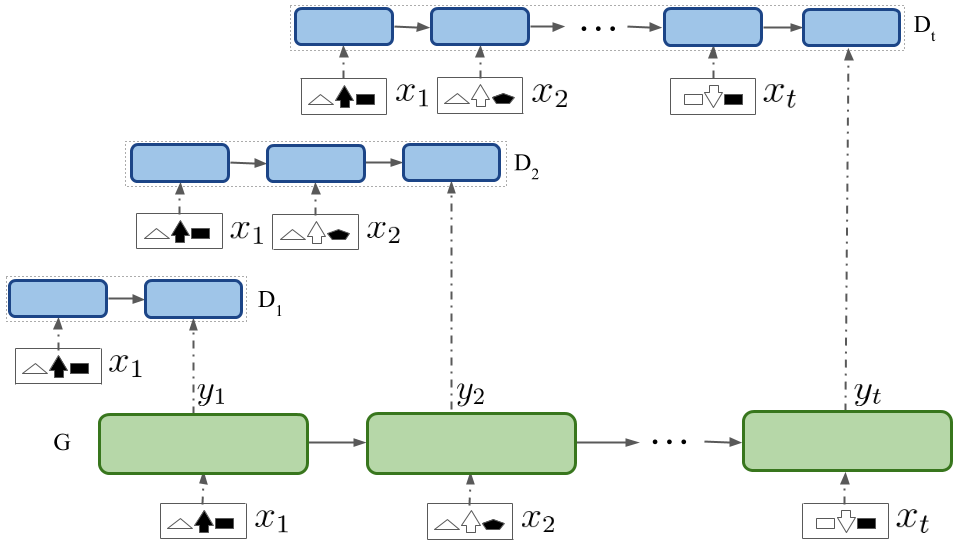
The above figure corresponds to our Context-RNN-GAN model, where the generator G and the discriminator D (where Di represents its ith timestep snapshot) are both RNNs. G generates an image at every timestep while D receives all the preceding images as context to decide whether the current image output by G is real vs generated for that particular timestep. xi are the input images.
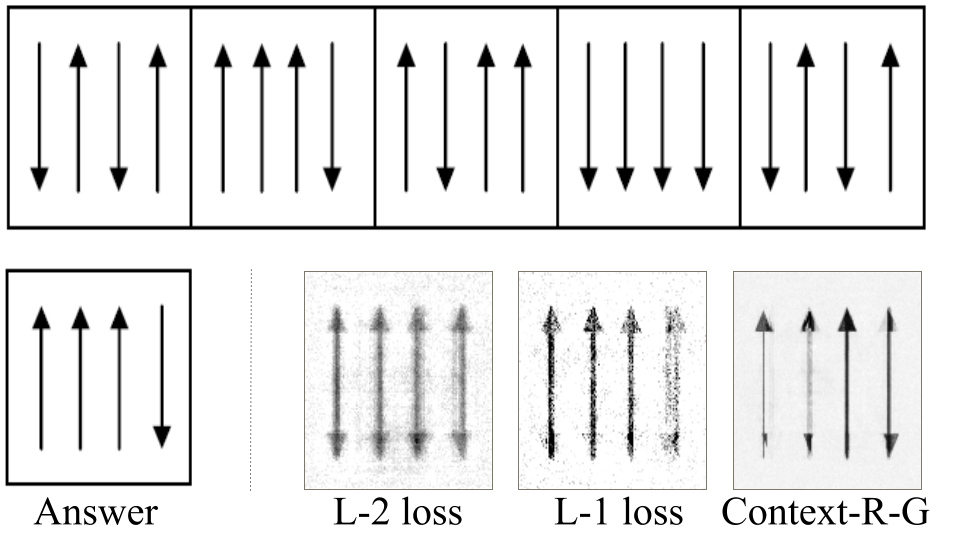
Impact of Adversarial Loss
When using an L-2 loss function, some of the generated images were superimpositions of the component parts and were too cluttered.
When using an L-1 loss function, although it was sharper than using an L-2 loss, it was missing some components of the actual diagrams.
A weighted combination of L-1 and adversarial loss (as defined for the context based discriminator model described above) was used for the Context-RNN-GAN model to produce the best results based on empirical evaluation.
Some Generations (Contextual-RNN-GAN)

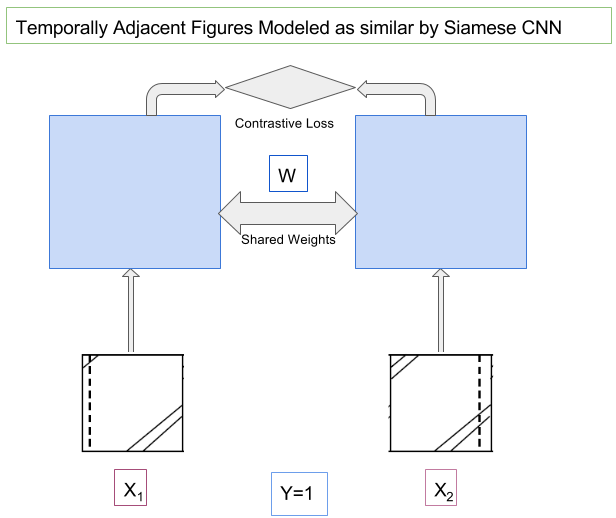
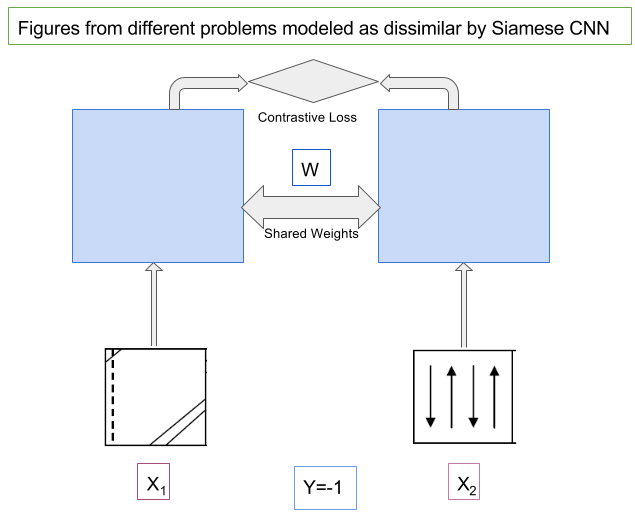
Modeling of Consecutive Timesteps using Siamese Networks for better accuracy
Comparison With Human Performance
| College-grade | 10th-grade | |
|---|---|---|
| Age range | 20-22 | 14-16 |
| #Students | 21 | 48 |
| Mean | 44.17% | 36.67% |
| Std | 16.67% | 17.67% |
| Max | 66.67% | 75.00% |
| Min | 8.33% | 8.33% |
Context-RNN-GAN with features obtained from Siamese CNN is competitive with humans in 10th grade in the sense that it is able to achieve accuracy of 35.4% when the generated features are compared with the features obtained from actual answer images. It needs to be noted that humans can see the options to get the best possible overall sequence of six images and hence can select the best choice while our model is just comparing the generations (obtained using sequence of five images in the problem) with options to get the best option. So, we can say that our model is very good generator and comparable to even 10th grade humans. An interesting aspect is that the model is never trained on the correct answers, it is just trained on multiple sequences from the problem images and still performs remarkably well.
Interesting Cases
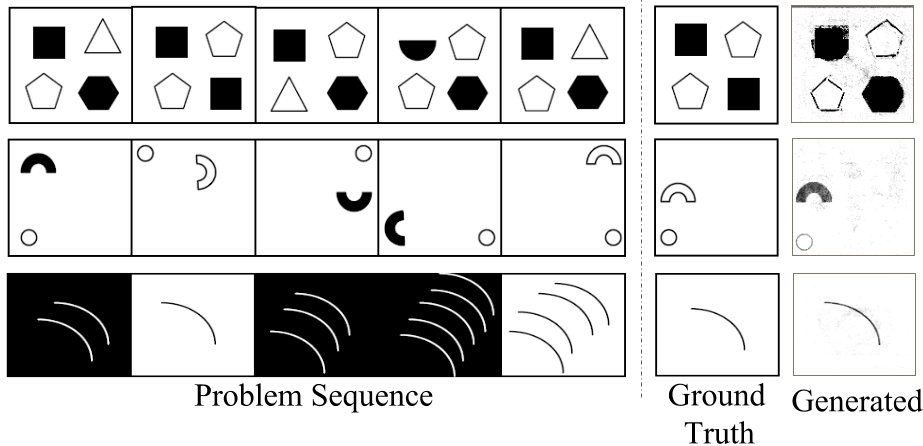
First Generation In the first example generation it is interesting to note that the model correctly predicted elements in off diagonal while faltered in the shape of the elements in leading diagonals.
Second Generation Second example shows an interesting case whereby the image generated by our model is also plausible (if by symmetry it is considered that first and third the semicircular ring is solid and hence fourth and sixth should be solid) while the actual answer is of course plausible according to the reasoning that the (solid vs hollow) flipped in the first two cases then stayed the same for the next two timesteps. Even more interesting is its analysis of the spatial dynamics of the ball and the semicircular ring which it almost correctly captured.
Third Generation Another very interesting case is the generation which it gets correct. However, in this case the answer figure is exactly similar to the second figure in the sequence. Therefore, it is not illustrative of the ability of the model to generate the sequence of the pattern.
Application of the model to Moving-MNIST
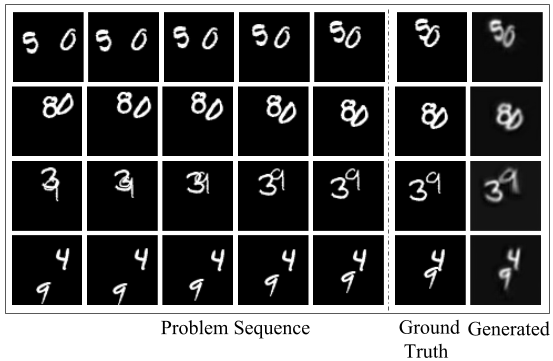
The model can be applied to video prediction tasks as illustrated by above figure. The Moving MNIST task consists of videos of two moving MNIST digits and the next frame has to be predicted from the preceding frames.